Parameter-uniform fractional step hybrid numerical scheme for 2D singularly perturbed parabolic convection–diffusion problems
Mathematics
The aim of underlying research work is to achieve higher-order uniformly convergent numerical approximation to the solutions of a class of singularly perturbed parabolic partial differential equations (PDEs). These types of model problems can be viewed, for instance, as the unsteady Navier-Stokes equation with large Reynolds number; and generally possess boundary layers. Due to the presence of the layer phenomena, the development of the fitted mesh methods (FMMs), which are uniformly convergent numerical methods constituted on special layer-adapted meshes, plays a key role to achieve accurate numerical results without much resolving the layers, even for smaller values of the perturbation parameter. In this regard, we develop and analyze an efficient fractional-step hybrid FMM for singularly perturbed multi-dimensional parabolic PDEs possessing regular boundary layers, with the emphasis of its theoretical and computational aspects. For approximating the time derivative, we use the Peaceman–Rachford fractional-step implicit method, and for the spatial discretization, a hybrid FMM is proposed on a special rectangular mesh which is tensor-product of piecewise-uniform Shishkin meshes in the spatial directions.
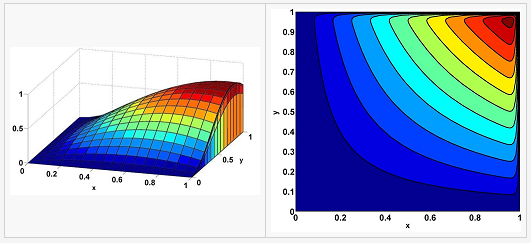
Caption: surface plot and contour plot of the numerical solution
The detailed work can be found in the following article:
Ref: Mukherjee, K. and Natesan, S, Parameter-uniform fractional step hybrid numerical scheme for 2D singularly perturbed parabolic convection–diffusion problems. J. Appl. Math. Comput., 60 (1-2), 51-86, (2019).