Approximations of fluid flow problems:
Mathematics
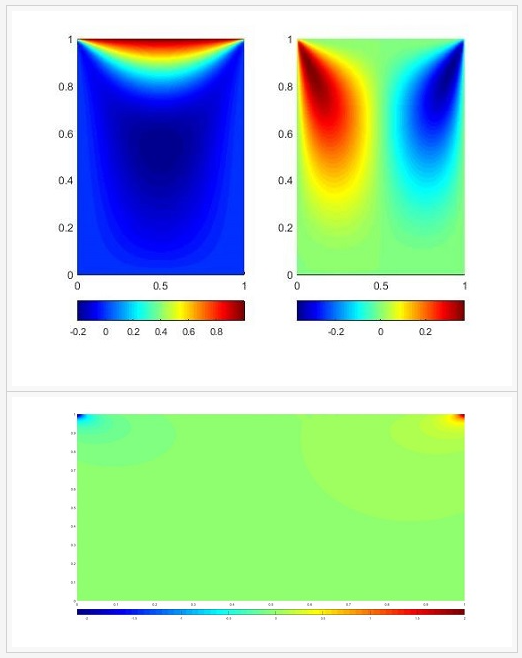
The mathematical model of fluid flow problems consists of coupled nonlinear partial differential equations, and hence obtaining analytical solutions or even closed-form solutions will be very difficult. Moreover, their numerical simulation in complicated scenarios (such as domains with diverse types of boundary and transmission conditions) remains far from trivial. Therefore, in collaboration with Prof. Ricardo Ruiz-Baier ( Monash University Australia), Prof. David Mora (University of Bio-Bio, Chile) and Prof Raimud Burger (University of Concepcion, Chile), I aim to develop a unified theoretical framework for the mathematical and numerical analysis of non-stationary fluid flow problems, and also other PDE-based models that appear in the coupling of fluid flow and transport problems. In particular, I work on the development (with emphasis on both theoretical and computational aspects) of numerical techniques such as Finite volume element methods, finite element methods, discontinuous Galerkin methods, which are used for obtaining an accurate and robust numerical solution of PDEs occurring in science and engineering with proper initial and boundary conditions. In view of the applicability of virtual element methods (VEMs) with polygonal meshes, VEMs are proven to be very impressive and have attracted the scientific community as far as a numerical approximation of PDEs on polygonal meshes is concerned. Therefore, recently I am focusing on designing suitable virtual element schemes for the approximation of PDEs that are defined on complex domains and polygonal meshes are used in the discretization of the domain. Recently, we have proposed new virtual element formulations for an approximation of nonstationary Stokes, Navier-Stokes, poroelasticity problems and related problems. For instance, the virtual element approximations for velocity and pressure of Lid-driven Cavity problems are shown in the following figure.
These study has been published in reputed international and details are as follows:
- Ref:Nitesh Verma and Sarvesh Kumar: : Lowest order virtual element approximations for transient Stokes problem on polygonal meshes, CALCOLO, 48(2021). https://doi.org/10.1007/s10092-021-00440-7.
- Ref:Raimund Burger, Sarvesh Kumar, David Mora, Ricardo Ruiz-Baier, and Nitesh Verma: Virtual element methods for the three-field formulation of time-dependent linear poroelasticity, Advances in Computational Mathematics, Vol 47 (2) (2021) ; https://doi.org/10.1007/s10444-020-09826-7.