Nonlinear dynamics of quantum systems
Physics
The dynamics of quantum systems play an essential role in quantum information processing and computing. We have studied the dynamics of superposition of wavepackets evolving under different nonlinear Hamiltonians corresponding to Kerr medium, Morse oscillator, and bosonic Josephson junction. We have shown that quantum systems' periodic, quasi-periodic, ergodic, and chaotic dynamics can change drastically if we change just the initial state to its superposition by keeping all other system parameters the same. Our initial analysis shows some relation between the interference of the initial state and its dynamics, but a detailed analysis is required to establish a definite connection between them.
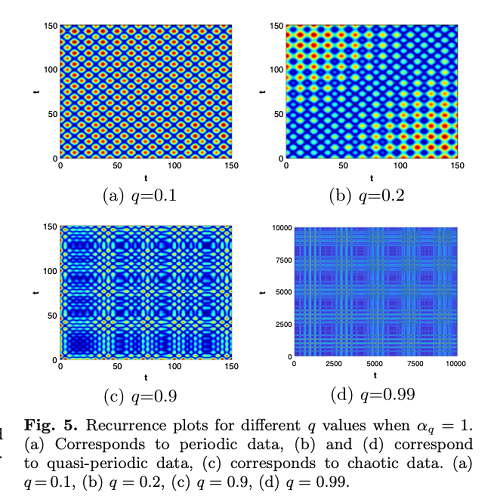
We attempted to understand how the q-deformation of ordinary Hamiltonian changes the system’s behaviour. The q-deformation confers non-linear properties to the ordinary quantum harmonic oscillator. By studying the dynamics of the resultant times series obtained for the expectation values of the dynamical variables, we conclude that the system studied exhibits periodic, quasi-periodic, and chaotic behaviour depending on the deformation parameter and the deformed coherent amplitude. As the deformation parameter and amplitude value increase, we observe that chaotic nature is the more prominent dynamical behaviour. For lower values of the parameters, the dynamical behaviour is mostly quasi-periodic.
Figure:- Recurrence plots for different q values when αq = 1. (a) Corresponds to periodic data, (b) and (d) correspond to quasi-periodic data, (c) corresponds to chaotic data. (a) q = 0.1, (b) q = 0.2, (c) q = 0.9, (d) q = 0.99.
- Ref: Dynamics of observables in a q-deformed harmonic oscillator, A. Pradeep, S. Anupama, C. Sudheesh, Eur. Phys. J. D. 74, 3 (2020), https://doi.org/10.1140/epjd/e2019-100436-y.
- Ref: Nonlinear dynamics of superposition of wavepackets, S. Kannan, M. Rohith, C. Sudheesh, Eur. Phys. J. Plus 137, 471 (2022), https://doi.org/10.1140/epjp/s13360-022-02673-z.