Multivariate Finite Support Phase Type Distributions 01/01/2025

Mathematics

Phase type (PH) distributions, which are defined on the non-negative real line, became quite popular in the last decades as they have been used in a wide range of applications of stochastic models. It forms a dense subset in the space of all distributions defined on the non-negative real numbers and at the same time it is numerically tractable because of its underlying Markovian structure. We could find a multivariate distribution, defined on any k-orthotope in [0,∞)k , having the analogous properties of the PH class. The new class is named Multivariate Finite Support Phase Type Distributions (MFSPH). We could study its properties and obtain an Expectation-Maximization algorithm to estimate the parameters of the distribution in the bivariate case. Also, we could demonstrate how this class could be used as approximations for bivariate finite support distributions by using simulated samples.

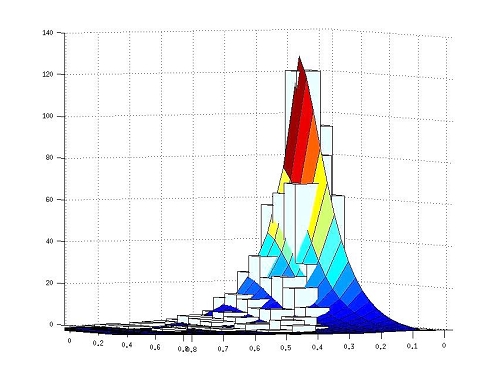
Figure 1: Bivariate finite support vector (X, Y), X a normalized G (2, 2) variate over [0, 1], Y = 0.5 X + ϵ, ϵ ̴ exp(1.5), fitted with BFSPH distribution of order 6 .