Deformed oscillators and quantum states of target space coordinates
We have found the quadrature operator eigenstates and wavefunctions for the general f-deformed oscillators. We have defined the f-deformed quadrature operator with the help of the homodyne detection method and represented its eigenstates in the f-deformed Fock state basis. This allowed us to produce a recurrence relation for the wavefunctions, which in turn allowed us to discover a new class of orthogonal polynomials. These new polynomials enabled us to represent the excited state wavefunctions of the f-oscillators in terms of the ground state wavefunction. Three types of deformed systems, namely math-type q-deformation, physics-type q-deformation, and (p,q)-deformation, were studied. We constructed the quantum states
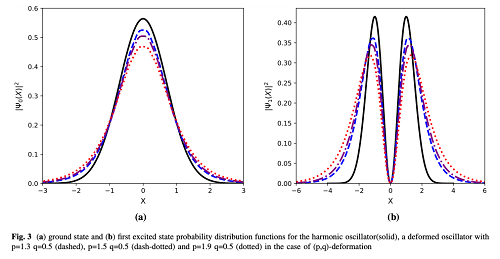
Figure:- (a) Ground state and (b) first excited state probability distribution functions for the harmonic oscillator (solid), a deformed oscillator with p=1.3 q=0.5 (dashed), p=1.5 q=0.5 (dash-dotted) and p=1.9 q=0.5 (dotted) in the case of (p,q)-deformation of target space coordinates from world-sheet states using quantum state tomography.
- Ref: Quadrature operator eigenstates and energy eigen functions of f-deformed oscillators, S. Anupama, A. Pradeep, A. Pal, C. Sudheesh, Indian J. Phys. (2022), https://doi.org/10.1007/s12648-022-02286-3.
- Ref: Construction of Quantum Target Space from World-Sheet States using Quantum State Tomography, SS Wani, A Shabir, JU Hassan, S Kannan, H Patel, C Sudheesh, M Faizal, Annals of Physics 441, 168867 (2022), https://doi.org/10.1016/j.aop.2022.168867