Virtual element method for the nonlinear convection-diffusion-reaction equation on Polygonal meshes 01/01/2025

Mathematics

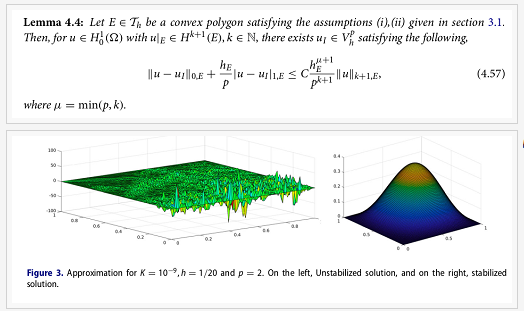
Virtual element method (VEM) is a newly born baby from Finite element method (FEM) Galerkin approach. In recent years, this method has been extensively studied for a variety of problems such as linear elliptic, parabolic, hyperbolic, stokes problems and so on. We are the first group to work on VEM in India. Our research work mainly focuses on the VEM discretization for the nonlinear equations. The major challenge in devising the computable VEM scheme is due to the fact that the basis functions are not known explicitly. We have formulated and solved a couple of nonlinear problems in this direction. Our most recent work is on the VEM discretization of the nonlinear convection-diffusion-reaction equation. We consider the Streamline upwind Petrov-Galerkin stabilization to reduce the non-physical oscillations present in the solution. We have performed the error analysis by showing the existence of the solution and derived the convergence estimates in the energy norm. Numerical experiments are conducted in order to validate the theoretical results. In this context we have proved an important result which is provided below,